引入

本次实验我们研究的是人口增长问题。人类作为真正意义上的食物链顶端，人口增长的结果会给一个国家，一个地区，甚至整个世界的运作带来很大的影响。是自然环境，资源，国防，劳动力等宏观问题变化的主要影响因素。认识人口数量的变化过程，建立数学模型描述人口的发展规律，做出较准确的增长预测，是制定积极、稳妥的人口政策的前提。所以研究人口的变化趋势是很有必要的。但是人口的变化不是一成不变的，它到底是符合怎么样的趋势在变化，这是本次实验的研究要点。本次使用的数据是美国从1790年到2000年每隔10年取样总共22年的数据。根据课本的指导，按照趋势匹配精度的增加，一共有四个模型（指数增长模型一，指数增长模型二，改进的指数增长模型和logistic模型）。本次实验所用的工具软件为MATLAB。

(注：

1. 本文的思路是完全按照《数学模型》第五版的思路进行的，数据略有不同，是因为这些数据是笔者亲自实验得出的结果。
2. 本文所用的数据同样来自《数学模型》第五版中人口增长模型提供的美国从1970年到2000年中每隔十年取一个的数据。)

指数增长模型一

模型假设

在最初的模型上，我们假设人口的年增长率在k年内是不会发生变化的。也没有任何的外力因数去影响人口的增长。

模型构建

如果已知今年的人口为$x_{0}$，年增长率为r，那么预测k年后的人口$x_{k}$为：

模型求解

使用MATLAB工具进行拟合，我们首先将该方程转化为线性方程。具体方法是在方程左右两边取对数，得

再通过变量替换，最后通过数据拟合求出对应的一阶线性方程，最后再将变量替换回来。

MATLAB代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

clc
clear
%输入t和x数据
t=0:22;
x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 105.7 122.8 131.7 150.7 179.3 203.2 226.5 248.7 281.4 308.7];

%xt=x0(1+t)^t 化为线性方程得：
%ln(xt)=ln(x0)+tln(1+r),其中xl=ln(xt),xl0=ln(x0),x=t,b=ln(1+r)
%利用一阶多项式线性拟合
xl=log(x);
p=polyfit(t,xl,1)
%得出该拟合的方程值
xp=polyval(p,t);
%求该拟合结果与线性方程真实值的标准差
A=[xl;xp];
xlxps=std(A);

%画图1,一阶多项式真实值与拟合值的对比
subplot(2,2,1)
plot(t,xp,':o',t,xl,'-*')
title('指数部分一阶多项式真实值与拟合值的对比','Color','r');
%画图2，一阶多项式真实值与拟合值的标准差
subplot(2,2,2)
plot(t,xlxps)
title('指数部分一阶多项式真实值与拟合值的标准差','Color','r');

%还原得原方程
X=exp(p(2)).*(exp(p(1)).^t);
r=exp(p(1))-1
x0=X(1)
%求该还原方程与真实值的标准差
B=[x;X];
Xxs=std(B);

%画图3，原方程与真实值的对比
subplot(2,2,3)
plot(t,X,':o',t,x,'-*')
title('原方程与真实值的对比','Color','r');
%画图4，原方程与真实值的标准差
subplot(2,2,4)
plot(t,Xxs)
title('原方程与真实值的标准差','Color','r');

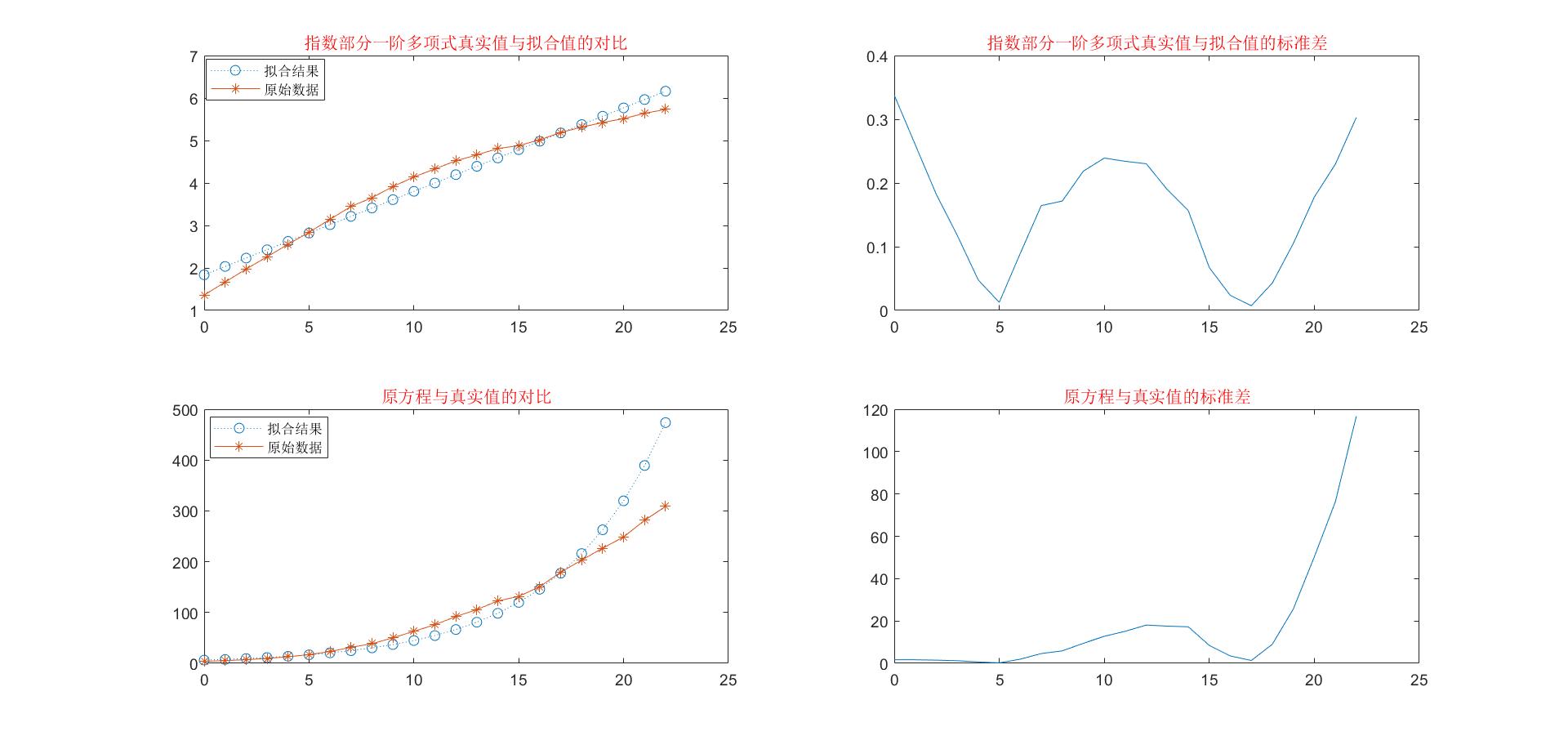
模型分析

通过图像我们可以看出，这种将增长率确定为不变的方法的拟合效果并不是非常好。虽然增长率的误差变化不大，但是最终得到的原方程拟合效果在18年后却完全脱离了实际情况。为了能够解决这种情况，接下来的指数增长模型二是将指数部分单独拟合。

指数增长模型二

模型假设

在这个模型中，我们对于人口增长的增长率分离出来单独进行拟合，同样的，本模型不考虑自然资源的限制对人口的增长的影响。

模型构建

当考察一个国家或一个较大地区的人口随时间延续而变化的规律时，为了利用微积分这一数学工具，可以将人口看做连续时间t的连续可微函数x(t)，记初始时刻（t=0）的人口为$x_{0}$，假设单位时间人口增长率为常数r，rx(t) 就是单位时间内x(t)的增长率$\frac{\mathrm{d} x}{\mathrm{d} t}$，于是得到 x(t) 满足的微分方程和初始条件

将该公式进行变量分离可以得出

当x>0时，人口将按指数规律无限增长。

模型求解

对于得到的常微分方程是比较容易人工得出 x(t) 的模型的，所以我们进行人工计算之后代入到MATLAB，$x_{0}$直接使用美国1970年的总人口3.9（单位：百万），r 是直接求取这21年的增长率平均值得到的。

MATLAB代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

clc
clear
%输入t和x数据
t=1:22;
x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 105.7 122.8 131.7 150.7 179.3 203.2 226.5 248.7 281.4];
xi=[0.2949 0.3113 0.2986 0.2969 0.2907 0.3012 0.3082 0.2452 0.2435 0.2420 0.2051 0.1914 0.1614 0.1457 0.1059 0.1059 0.1579 0.1464 0.1161 0.1004 0.1104 0.1349];
r=mean(xi);

%xt=x0exp(rt) 通过求解常微分方程得：
X2=(39.*exp((513.*t)/2500))/10

%求该还原方程与真实值的标准差
B2=[x;X2];
X2xs=std(B2);

%画图1，原方程与真实值的对比
subplot(1,2,1)
plot(t,X2,':o',t,x,'-*')
title('原方程与真实值的对比','Color','r');
%画图2，原方程与真实值的标准差
subplot(1,2,2)
plot(t,X2xs)
title('原方程与真实值的标准差','Color','r');

%其中常微分方程求解代码如下
clc
clear

syms x(t)
eqn = diff(x,t) == 0.2052*x;%r=0.2052
con = x(0) ==3.9;
X2 = dsolve(eqn,con)

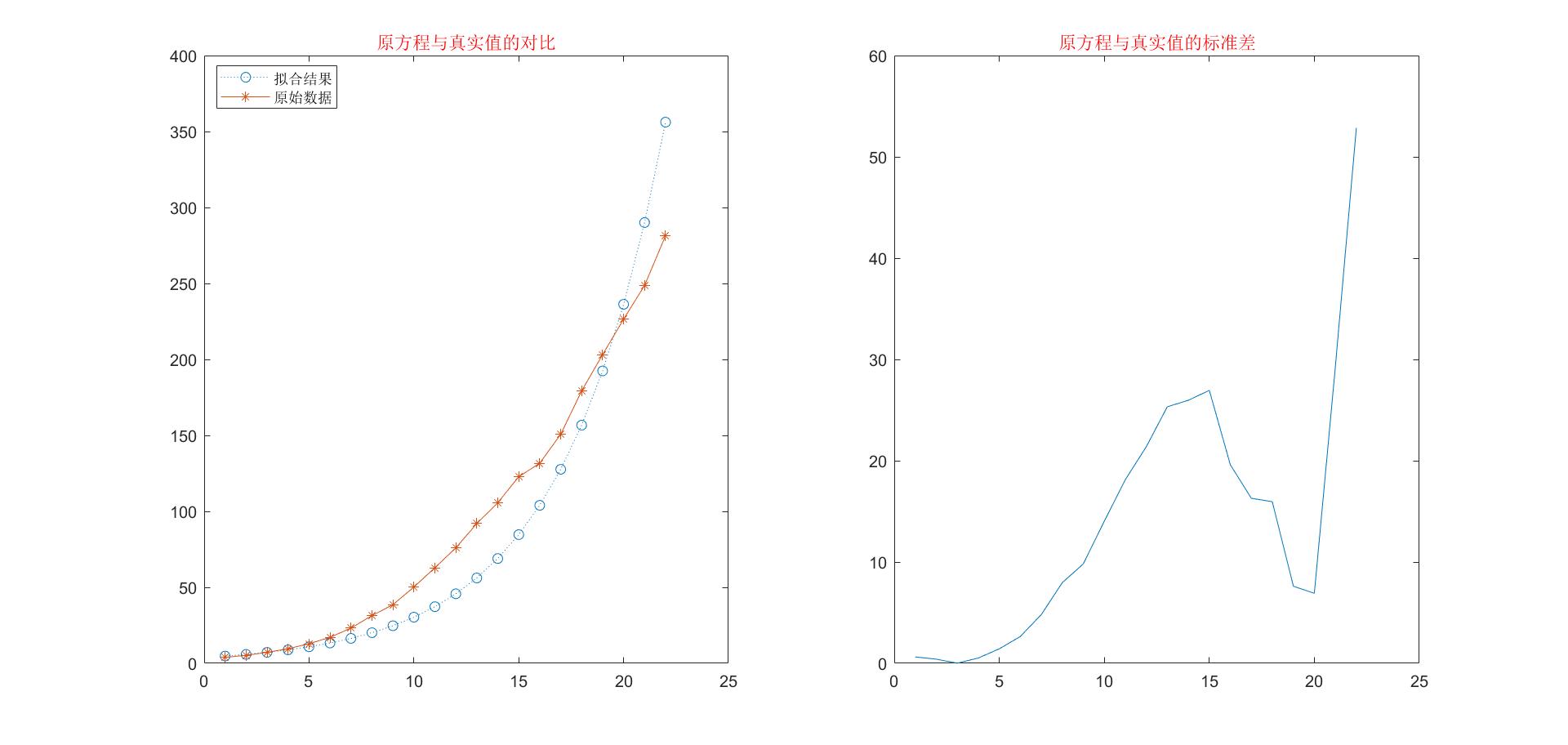
模型分析

从标准差图像中我们可以看出：该模型比指数增长模型一的标准差要小很多，要更加贴合实际，但是在14年左右还是出现较大的误差，然后也存在在20年之后模型完全脱离实际的情况。所以为了能够更好地贴合实际，我们将指数部分再一次进行优化。

改进后的指数增长模型

建模假设

由于增长率不是一成不变的，所以我们对之前的模型进行重新的修改，将指数部分进行线性拟合，同时还是不考虑自然资源限制对人口增长的影响。

模型构建：

我们将指数增长模型二改写为

其中，令r为一个线性函数

模型求解

使用MATLAB中的Curve Fitting Tool进行线性拟合得出$r_{1}=-0.0114,r_{0}=0.3252$

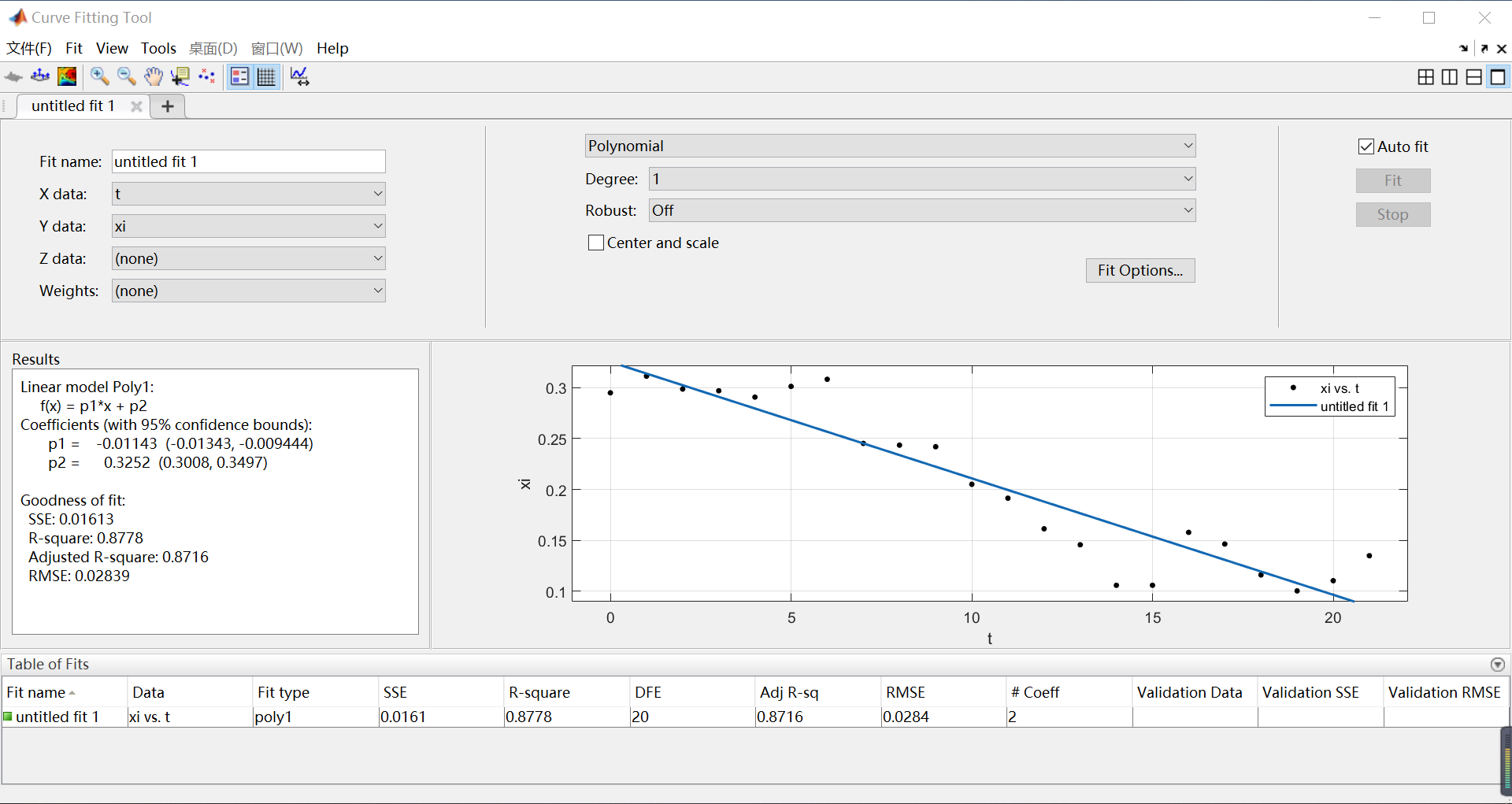
将该数据带入到MATLAB中常微分方程的求解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

clc
clear

syms x(t)
eqn = diff(x,t) == (-0.0114*t+0.3252)*x;
con = x(0) ==3.9;
X3 = dsolve(eqn,con)

%得到拟合方程
X=(39*exp(-(3*t*(19*t - 1084))/10000))/10

具体MATLAB代码如下
clc
clear
%输入x和y数据
t=0:21;
x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 105.7 122.8 131.7 150.7 179.3 203.2 226.5 248.7 281.4];
xi=[0.2949 0.3113 0.2986 0.2969 0.2907 0.3012 0.3082 0.2452 0.2435 0.2420 0.2051 0.1914 0.1614 0.1457 0.1059 0.1059 0.1579 0.1464 0.1161 0.1004 0.1104 0.1349]

X3=(39.*exp(-(3.*t.*(19.*t - 1084))/10000))/10

%求该拟合结果与真实值的标准差
A3=[x;X3];
X3xs=std(A3);

%画图1，原方程与真实值的对比
subplot(1,2,1)
plot(t,X3,':o',t,x,'-*')
title('原方程与真实值的对比','Color','r');
%画图2，原方程与真实值的标准差
subplot(1,2,2)
plot(t,X3xs)
title('原方程与真实值的标准差','Color','r');

结果如下图：

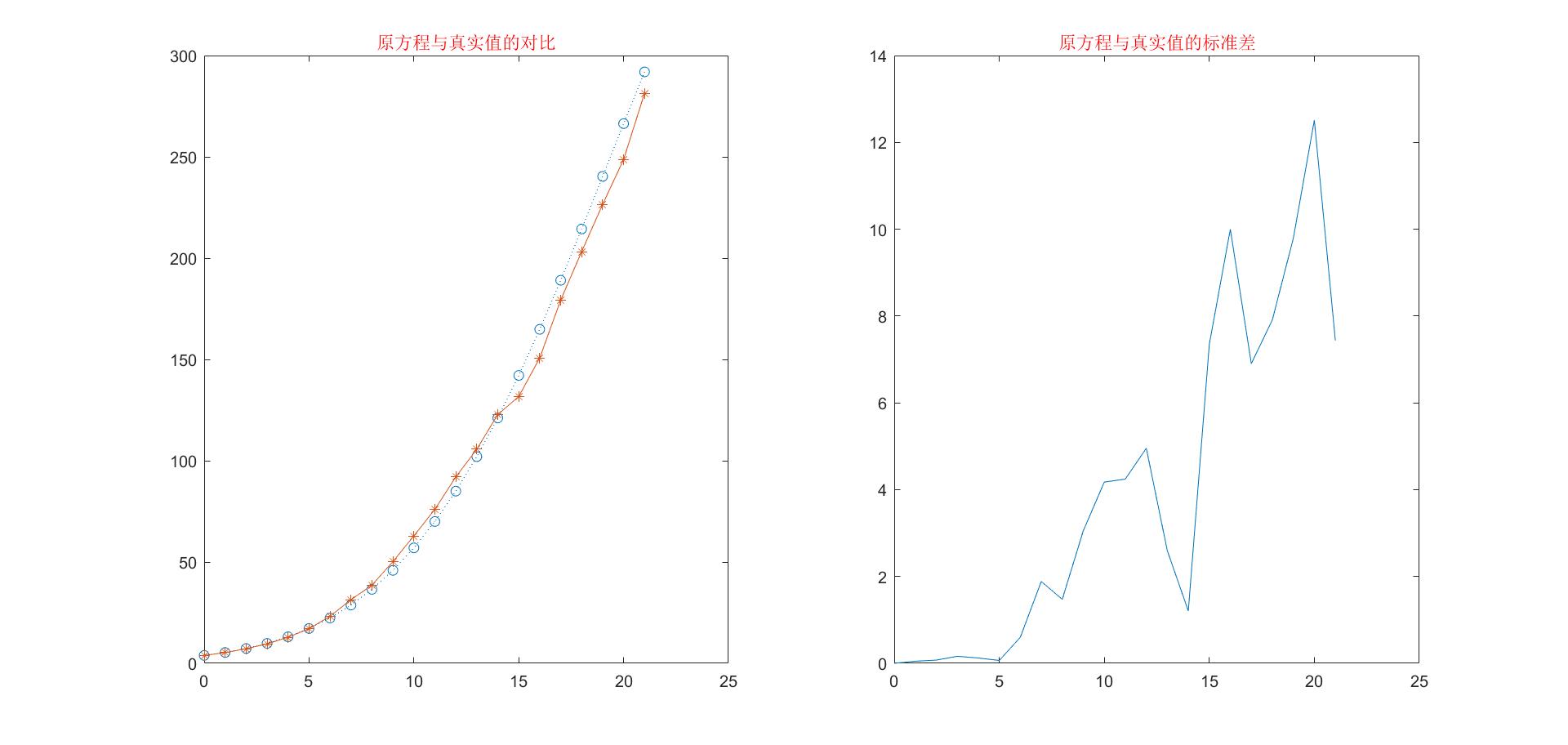
模型分析

从该模型的结果我们可以看出，拟合数据和实际数据的标准差已经缩减的很小了，从左图中也可以很直观地看出两条曲线非常接近。虽然改进的指数增长模型考虑到增长率随时间的变化，计算结果有所改善，但是它没有反应增长率下降的原因，增长率行数形式也呈现出不确定性，给应用带来不便，为了建立更加符合实际情况的人口增长模型，必须考虑人口下降的机理，修改原来的模型假设。

至此，三个模型的结果如下：

logistics模型

建模假设

关于人口增长到一定数量之后增长率下降的原因，查阅资料知道：自然资源、环境条件等因数对人口增长起着阻滞作用，并且随着人口的增加，阻滞作用越来越大。所以才产生了logistic模型。

模型构建

资源和环境对人口增长的阻滞作用体现在对增长率 r 的影响上，使 r 随着人口数量 x 的增加而下降。将 r 表示为含 x 的函数 r(x) ,并且取既简单又方便应用的线性减函数 $r(x)=a+bx$。为了赋予增长率函数 r(x) 中系数a，b 以实际含义，引入两个参数：

1. 内禀增长率r  r是（理论上）x=0的增长率，即r(0)=r，于是a=r；

2. 人口容量$x_{m}$  $x_{m}$是资源和环境所能容纳的最大人口数量，当x=$x_{m}$时人口不再增长，即$r(x_{m} )=r+bx_{m}=0$，得到$b=- \frac{x}{x_{m}}$

    

由此导出的增长率函数为$r(x)=r(1-\frac{x}{x_{m}})$。用 r(x) 代替指数增长模型二中的r，得到

方程右端的因子$rx$体现人口自身的增长趋势，因子$(1-\frac{x}{x_{m}})$则体现了资源和环境对人口增长的阻滞作用。显然 x 越大，前一因子越大，后一因子越小，人口增长是两个因子共同作用的结果。

模型求解

我们将常微分方程通过变量分离可以得到

其中$r，x_{0}，x_{m}$为参数。

估计参数方法一

将常微分方程改写为

对于右端的 x 用线性最小二乘法估计$r和x_{m}，x_{0}$ 直接采用原始数据。

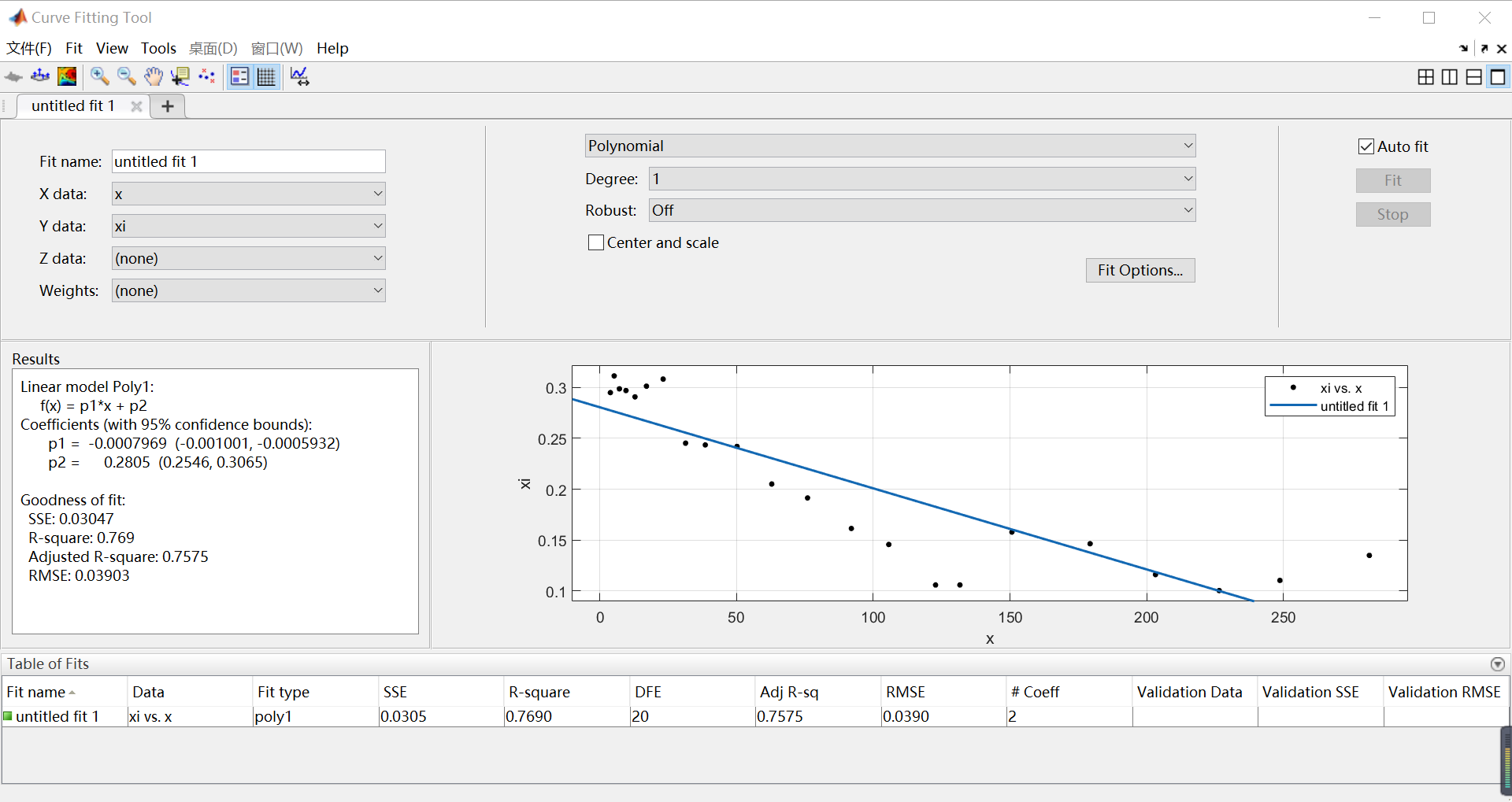
图中 x 为人口数量，xi为增长率。通过Curve Fitting Tool线性拟合，我们可以得到$a=r=p2=0.2805,b=p1=-0.0007969$，通过$b=- \frac{x}{x_{m}}$ ，得到$x_{m}=352.0$，再取$x_{0}=3.9$得到模型。具体MATLAB代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

clc
clear
%y是实际的人口数量，yx是用符号求常微分方程的方程，x是ode45拟合后的人口数量
%ty，tx，t分别是y，yx，x下的横坐标
ty=0:21;
tx=0:48;
y=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 105.7 122.8 131.7 150.7 179.3 203.2 226.5 248.7 281.4];

%这里的常微分方程的解在另一个脚本求得
yx=352./(exp(log(3481./39) - (561*tx)./2000) + 1);

%这里是求真实值y和拟合值yx的标准差
A=[y;yx(1:22)];
B=std(A);
D=mean(B)

%画图
subplot(2,1,1)
plot(tx,yx,'-o',ty,y,'-*');
axis([0 50 0 360]); 
subplot(2,1,2)
plot(ty,B)
axis([0 50 0 18]);

%其中常微分方程的代码如下
clc
clear

syms yx(t)
eqn = diff(yx,t) == 0.2805.*yx.*(1-yx./352);
con = yx(0) ==3.9;
yS = dsolve(eqn,con)

估计参数方法二

直接使用人口数据和非线性最小二乘法估计$r，x_{0}，x_{m}$。

得出$r=0.2155,x_{m}=443.9940,x_{0}=7.6963$,代入原方程得出模型。

具体代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

clc
clear
%x是实际的人口数量，yx是用符号求常微分方程的方程
%tx，t分别是yx，x下的横坐标
t=0:21;
tx=0:48;
x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 105.7 122.8 131.7 150.7 179.3 203.2 226.5 248.7 281.4];

x0=[444 7.7 0.22];
fun = @(k,t)k(1)./(1+((k(1)./k(2))-1).*exp(-k(3).*t));
k = lsqcurvefit(fun,x0,t,x) 
%这里的常微分方程的解在另一个脚本求得
yx=k(1)./(1+(k(1)./k(2)-1).*exp(-k(3).*tx));
%这里是求真实值y和拟合值yx的标准差
A=[x;yx(1:22)];
B=std(A);
D=mean(B)

%画图
subplot(2,1,1)
plot(tx,yx,'-o',t,x,'-*');
title('原方程与真实值的对比','Color','r');
axis([0 50 0 450]); 
subplot(2,1,2)
plot(t,B)
title('原方程与真实值的标准差','Color','r');
axis([0 50 0 6]);

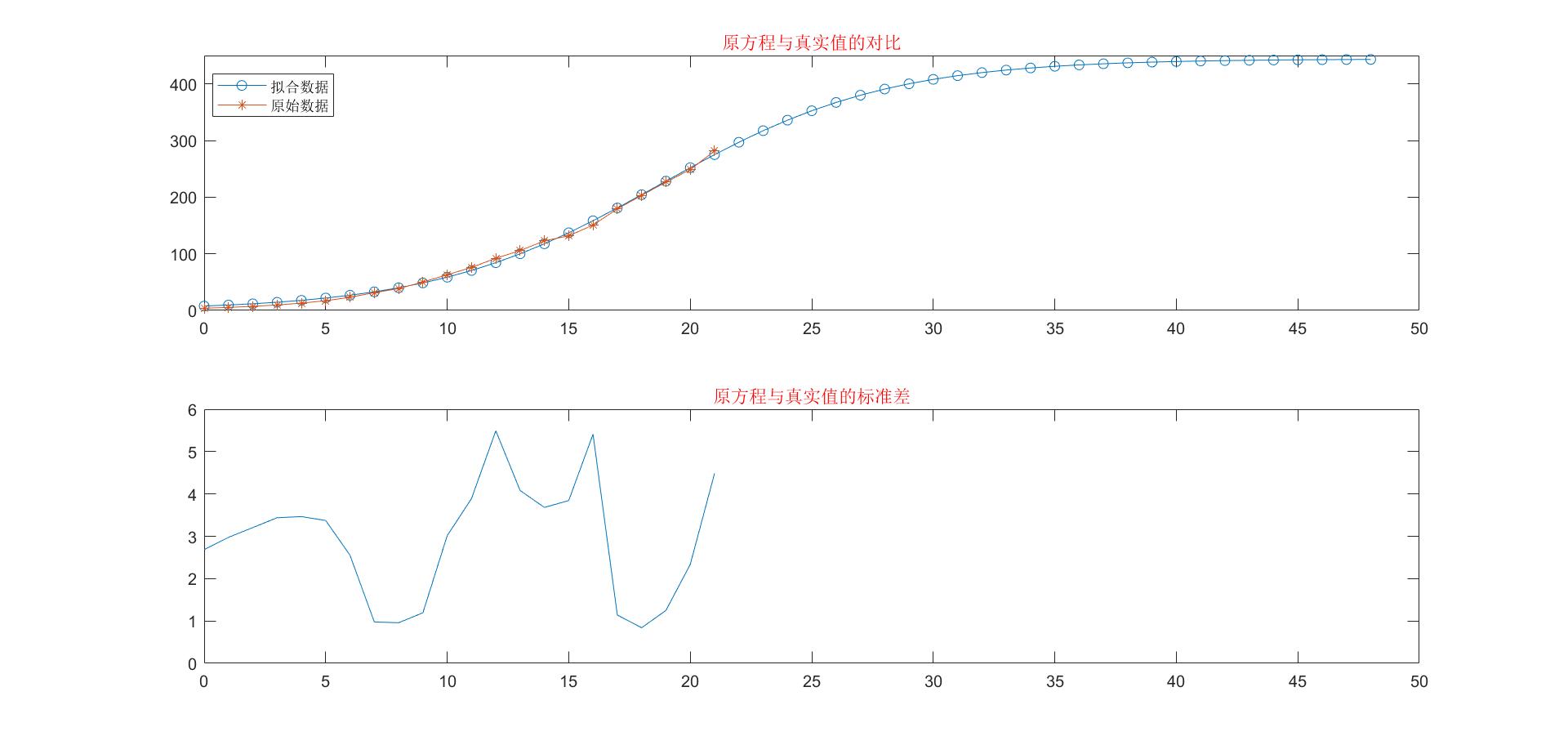
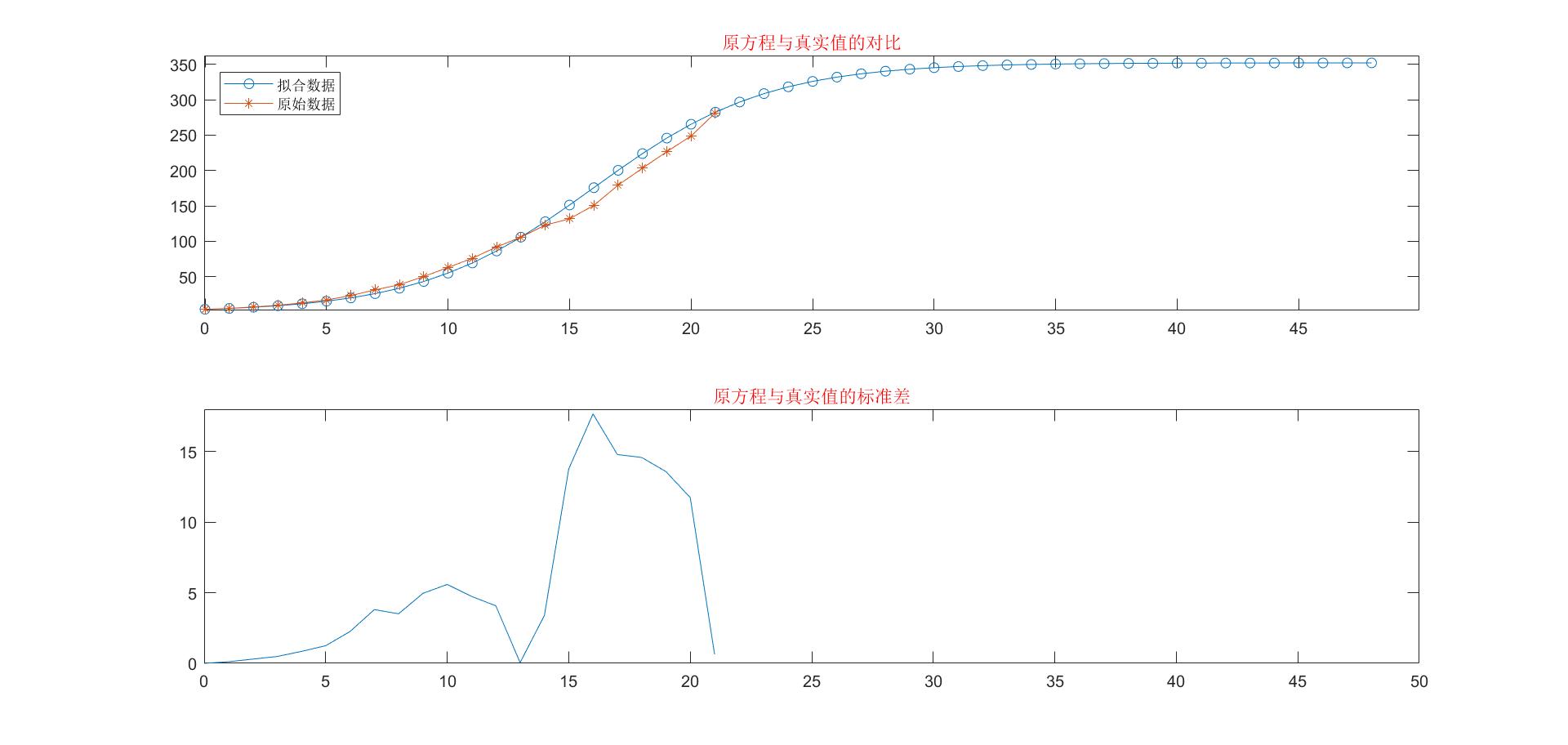
两个方法的拟合结果如下图：

模型分析

首先，对于logistic模型，应该给予比较高的评价，该模型在生态系统的种群研究中有很大的价值。该模型对美国人口的趋势预测也比较准确。接下来对于方法一和方法二的分析：从标准差结果可以看的出来，非线性最小二乘法拟合的结果（即方法二）比线性最小二乘法拟合（即方法一）要好，二的标准差控制在6以内，是一个相对准确的结果了。但是就预测的结果来看，在预测2010年美国的人口数量的时候，方法一要更加准确，方法二预测的结果反而比较大了（414.48），是不符合实际的，这里笔者觉得会不会是出现过拟合的现象，又或者是出现了新的影响因素。这可能需要进一步研究。

实验总结

1. 对于建立模型的方法，在本节中，我们可以很清楚地认识到要想建立一个非常接近现实的模型是不简单的，我们最开始需要根据该现实问题最大的影响因数提取出来，其他条件理想化，然后建立起该主要因数影响的模型。再通过逐步添加其他的次要的影响因数，逐步建立起较为完善的模型。

2. 其次，在建立模型的过程，我们也可以用一些比较简单的方程，比如我们在完善logistic模型的时候对于指数部分的拟合，一开始是使用简单的线性拟合，然后再是二次方程拟合，最后又进行非线性最小二乘法拟合，一步步得到比较精确的模型。

3. 判断一个模型的准确程度，用模型来预测一些已知的结果是一种非常好的方式。但是，我们也可以通过改变模型的参数，通过判断模型的变化是否与现实相符，这样一来还可以协助判断某些参数在现实中的意义。

4. Logistic模型是生物系统中对种群数量进行预测的一个非常经典的模型，通过该模型我们清楚认识到种群数量的增长不是按照指数的增长方式来的，他会有一些限制（包括环境情况，资源等），最后趋向一个平衡。这对我们研究种群的数量变化为人类的生产发展提供参考。同时适用于外来生物入侵的现象，也可以为解决繁殖泛滥的解决方法提供理论基础。

今日的分享就到这里啦，大家有什么想法都可以在评论区讨论~~

每一条我都会很认真看的，谢谢大家~~

参考文献：《数学模型》第五版，姜启源、谢金星、叶俊编，国际标准书号ISBN：9787040496314 第五章：微分方程模型

（本文为原创作品，未经许可禁止转载！）

• ← Previous Post
• Next Post →